By Ivan Savin[*]
The model of replicator dynamics as an evolutionary theory of competition between firms in economics is widely used. I describe how to test this model based on empirical data, as well as the advantages and disadvantages of these tests. Furthermore, I describe ways on how to improve the model of replicator dynamics taking into account global value chains and using the world input-output database, which helps to obtain more thorough and accurate results.[1]
The world we live in is constantly evolving - sometimes smoothly, and sometimes very abruptly. Just recall several industrial revolutions our society has experienced over the past three centuries, and how much people’s lifestyle has changed during this time. New ideas, often not only of a technological nature, and related innovations are the main driving force of these changes. Analysing these changes is a difficult task, since we are trying to understand both short-term and long-term patterns and causes of emerging changes, the nature of those participants who create, implement, disseminate knowledge, and compete with each other. To address these issues, a conceptual framework is needed.
The economic literature offers two alternative approaches to understanding the dynamics described. The first one proposes a rather complex system based on understanding (at times, unlimitedly) rational agents and determining the equilibrium states between them. Within this framework, the economy develops on the basis of clear laws (similar to physics) and almost always is in an “equilibrium” state, where economic agents act in an optimal way to achieve the best result for themselves, taking into account the response of their competitors and making an accurate forecast of future events. This approach is often referred to as neoclassical, and dynamic stochastic general equilibrium models are its good example. The second concept presents the economy as an ecosystem that does not always act and react in a predictable way; economic dynamics is the result of activities devoted to experimentation in a poorly understood environment, often faced with uncertainty. This approach is called evolutionary in the economic literature, and one of the fundamental works on this topic is the book written by Nelson and Winter (1982).
The idea of comparing the evolutionary development of the economy with the evolutionary development of living organisms on earth is far from new. Some people argue that Charles Darwin borrowed some ideas from Adam Smith when he formulated the theory of natural selection. “Darwin's theory does not defend any higher principles, except for the pursuit by individuals of their own interests, i.e. passing on your own genes to future generations. The problem is similar to the one faced by Adam Smith when he advocated laissez faire as the surest path to a harmonious economy. Smith argued that an ideal economy may appear orderly and well-balanced, but it will arise “naturally” from the interaction of people who follow no path other than pursuing their own interests” (Gould, 1975, pp. 99-100).
Drawing analogy between nature and economics, random variation at the gene level can be represented as inventions and innovations that create companies, while natural selection - as competitive market selection. The selection units are not different species, but firms or even entire industries. The key model within this approach was the model of replicator dynamics, first formalized by Taylor and Jonker (1978) as a model for selecting the best behaviour strategies, and later used as a model of competition between economic actors (Metcalfe, 1994) or between alternative views in public opinion (van den Bergh et al., 2019). The replicator dynamics model is represented in the following equation:
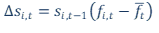 (1)
(1)
where is the difference between two years; is the share of firm i in the time period t on the market; is the form of measuring (“fitness” of the company i in the period t to the given market (this can be the cost per unit of production, product quality, labour productivity of the company, etc.); - weighted average (relative to the company's market share) "fitness" of firms on the market. According to equation (1), firms with above average fitness should increase their market share and vice versa. This model quickly gained widespread popularity and is used as an integral part of many studies (Mazzucato, 1998; Foramitti et al., 2021).
The logical question is how to test the seemingly logical economic law on the basis of real data. There are several ways. The first and most common of them is to take a certain market and decompose the change in aggregated "fitness" into two components:
– change in "fitness" at the level of individual firms (within-effect), when firms increase quality and reduce costs through innovation, which leads to an increase in "fitness" at the level of the entire industry;
– redistribution of market shares among its participants (between-effect), when without any growth of "fitness" at the level of firms it is possible to achieve an increase in the aggregate indicator. The between-effect indicates the presence of market competition in the economy.
For ease of interpretation, these two effects are normalized to their sum to unity. Thus, the magnitude of each effect reflects their proportional contribution to the growth of fitness at the industry level. This approach has been applied to different countries, time periods and sectors of the economy and showed a very heterogeneous picture, where competition could be present (to a small extent) in some sectors and completely absent in others (see Cantner et al., 2019). Most often, the estimate of the normalized between-effect fluctuated around zero on average and, with rare exceptions, did not exceed 10% for a particular period or sector of the economy.
In addition to a number of shortcomings that are valid not only for this method, which I will describe in detail below, an obvious drawback of the decomposition method is the fact that market shares here are traditionally expressed not through the sales of firms, but through the amount of labour employed. Since sales growth today does not have to lead to an increase in the number of employees, this limitation raised many questions. The answer to this criticism was a direct econometric estimation of equation (1), where sales of firms are on the left side of the equation, and the level and dynamics of "fitness" of these companies are taken as explanatory variables on the right, as well as fixed effects at the level of both companies and the time periods over which the estimate is made. Since such a regression model is estimated for each industry separately, the effect of competition on firm growth, taking into account fixed time variables, is equivalent to estimating their deviation from the industry average for each year, which in turn is equivalent to equation (1). The key parameter for evaluating here is the proportion of the variance in sales growth that can be explained using the fitness variables, i.e. how well do these variables explain the dynamics of a company's sales. This approach was first applied by Bottazzi et al. (2010) to data for France and Italy, followed by Dosi et al. (2015) - to data for the USA, Germany, France and the United Kingdom. Here, the assessment of the contribution of competition to sales growth fluctuated on average within 10–20%, which is higher than the estimates obtained on the basis of the decomposition method, but still very modest.
A third way to assess the role of competition in the economy, which complements rather than replaces the first two, is to assess the heterogeneity of companies in terms of their fitness in each industry and examine how this value changes over time. The idea is that if there is a healthy economic competition, the difference in productivity between firms should remain small and not increase over time. Otherwise, the data indicate that a significant part of companies can maintain a market niche, even being many times less productive than their competitors. In the literature, such companies are sometimes called “zombie companies” (McGowan, Andrews, Millot, 2017; Savin, 2020). Note that presence of “zombies” inhibits economic growth, since these firms divert to themselves a significant share of demand, as well as resources, which could be more effectively used in the economy. For example, Dosi et al. (2015) showed that in the United States, a company with one standard deviation below the industry average is 3 times less productive than a company that is one standard deviation above this average. For developing economies (such as India and China), this difference reaches factor 7 (Dosi et al., 2017). In Russia, the spread in labour productivity between companies is of factor 30. This spread increased continuously from 2006 to 2015, and only in 2016–2017 dropped slightly (Savin et al. 2020).
When using and interpreting the methods for measuring competitive selection described above, it is important to remember that they all have a number of common drawbacks, which I would like to address in more detail.
First, the replicator dynamics model indicates competition for the same consumer who chooses among all the sellers represented. However, with the exception of rare cases where it is possible to manually identify all manufacturers on a separate market, there is no real opportunity to divide all companies according to the markets in which they actually compete with each other. The sectoral division (e.g. NACE) is very imprecise. However, even increasing its detail from two-digit to four-digit does not help to solve the problem (see examples presented in Savin et al., 2019).
The second problem arises from the uncertainty of what to accept as the "fitness" of the company. The literature knows examples of the use of revenue and profitability per employee, labour productivity and total factor productivity (TFP), and this list is not yet complete. Mariev et al. (2020) compared the above indicators in relation to Russian data and concluded that they all demonstrate fairly similar results, at least for the decomposition method of the industry aggregated at the “fitness” level. Lately, the indicator of labour productivity has been used somewhat more often. Unlike revenue, it takes into account the heterogeneity of production costs, but in contrast to TFP does not imply the strong assumption that firms using different technologies experience the same synergies between factors of production.
Third, the replicator dynamics model assumes that firm's success is determined by the difference between its "fitness" and the "fitness" of its competitors. But today, economic agents rarely independently carry out the entire cycle of production of goods or services. Companies are embedded in complex value chains, and while in reality consumers choose between products, equation (1) assumes that the choice is made between companies. Cantner et al. (2019) proposed expanding the replicator dynamics model to include all of its suppliers in the firm's fitness calculation. We analysed a simplified case when value chains have the same number of vertically integrated markets (i.e., the number of links in the value chain is strictly the same), and only one company operates in each market in the value chain, while the fitness of companies is heterogeneous and they cannot change one supplier for another (for example, due to the presence of long-term contracts). Using this example, we have shown that the proposed model is able to explain the puzzling empirical evidence even when there is competition between companies in the end-user market. The reason for this lies in firm dependence on their suppliers. In other words, firm A will lose the competition to firm B, being more productive itself, but having less competitive suppliers.
Failing to find sufficiently detailed firm-level data to empirically validate the extended model of replicator dynamics, Mundt et al. (2021) conducted recently a study based on World Input-Output Data (WIOD). According to these data, in each specific sector of the economy, countries compete for global market share. We can calculate the added value and labour costs associated with its creation, which from a particular industry of one country come in the form of goods and services to a certain industry of another country. The estimates we obtained show a significant increase both in the value of the between effect and the proportion of the variance in sales growth explained by labour productivity factors. This indicates that the previously presented estimates of competitive selection must have been underestimated. In other words, the value of the "between" effect obtained for Italy earlier and fluctuating around zero, as well as the explanatory ability of the factors of "fitness" in the regression model at the level of 10% is lower than if we estimate the model of replicative dynamics taking into account global value chains. The extended replicator dynamics model taking value chain linkages into account presents an important step forward in measuring market selection and also an innovative way of using the WIOD data on global value chains.
References
Bottazzi G., Dosi G., Jacoby N., Secchi A. and Tamagni F. (2010). Corporate performances and market selection: Some comparative evidence. Industrial and Corporate Change, 19, 1953–1996.
Cantner U., Savin I. and Vannuccini S. (2019). Replicator dynamics in value chains: Explaining some puzzles of market selection. Industrial and Corporate Change, 28 (3), 589–611 https://doi.org/10.1093/icc/dty060 .
Dosi G., Luna I., Mathew N., Netto E.Y.H., Savin I. and Yu X. (2017). Productivity, market selection and corporate growth: Comparative evidence from BRIC nations. Proceedings of the 5th CONCORDi conference in Seville, September 2017.
Dosi G., Moschella D., Pugliese E. and Tamagni F. (2015). Productivity, market selection, and corporate growth: Comparative evidence across US and Europe. Small Business Economics, 45, 643–672.
Foramitti J., Savin I. and van den Bergh J. (2021). Emission tax vs. permit trading under bounded rationality and dynamic markets, Energy Policy, 148(B): 112009 https://doi.org/10.1016/j.enpol.2020.112009
Gould S.J. (1975). Ever since Darwin: Reflections in natural history. N.Y.: Norton & Company.
Mazzucato M. (1998). A computational model of economies of scale and market share instability. Structural Change and Economic Dynamics, 9 (1), 55–83.
Mariev O.S., Pushkarev A.A. and Savin I.V. (2020). Estimating market selection in Russia: Comparative Analysis of Different Performance Indicators. Proceedings of the 8th conference international conference Innovation Management, Entrepreneurship and Sustainability https://www.webofscience.com/wos/woscc/full-record/WOS:000589725700029?SID=8DkAH1ziHprp79pwhWV
McGowan M.A., Andrews D. and Millot V. (2017). The walking dead? Zombie firms and productivity performance in OECD countries OECD Economics Department. Working Papers, No. 1372.
Metcalfe J.S. (1994). Competition, Fisher’s principle and increasing returns in the selection process. Journal of Evolutionary Economics, 4 (4), 327–346.
Mundt P., Cantner U., Inoue H., Savin I. and Vannuccini S. (2021). Market selection in global value chains. BERG Working Paper Series, No. 170 http://hdl.handle.net/10419/234123
Nelson R.R. and Winter S. (1982). An evolutionary theory of economic change. Cambridge: Harvard University Press.
Savin I. (2020) Studying market selection in Russia and abroad: Measurement problems, national specificity and stimulating methods, Journal of the New Economic Association, 48 (4):197-204 (In Russ.) https://doi.org/10.31737/2221-2264-2020-48-4-9
Savin I.V., Mariev O.S. and Pushkarev A.A. (2019). Survival of the fittest? Measuring the strength of market selection on the example of the Urals Federal District. The HSE Economic Journal, 23, 1, 90–117. https://doi.org/10.17323/1813-8691-2019-23-1-90-117 (in Russian).
Savin I.V., Mariev O.S. and Pushkarev A.A. (2020). Measuring the strength of market selection in Russia: When the (firm) size matters. Voprosy Ekonomiki, 2, 101–124. https://doi.org/10.32609/0042-8736-2020-2-101-124 (in Russian).
Taylor P. and Jonker L. (1978). Evolutionary stable strategies and game dynamics. Mathematical Biosciences, 40, 145–156.
van den Bergh J.C.J.M., Savin I. and Drews S. (2019). Evolution of opinions in the growth-vs-environment debate: Extended replicator dynamics. Futures, 109, 84–100. https://doi.org/10.1016/j.futures.2019.02.024
[*] Institute of Environmental Science and Technology, Universitat Autònoma de Barcelona, Spain:
[1] The author acknowledges support from the Russian Science Foundation (RSF grant number 19-18-00262).